一场比赛中共有 n 支队伍,按从 0 到 n - 1 编号。
给你一个下标从 0 开始、大小为 n * n 的二维布尔矩阵 grid 。对于满足 0 <= i, j <= n - 1 且 i != j 的所有 i, j :如果 grid[i][j] == 1,那么 i 队比 j 队 强 ;否则,j 队比 i 队 强 。
在这场比赛中,如果不存在某支强于 a 队的队伍,则认为 a 队将会是 冠军 。
返回这场比赛中将会成为冠军的队伍。
示例 1:
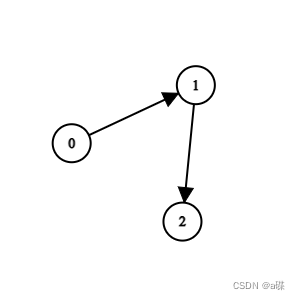
输入:grid = [[0,1],[0,0]]
输出:0
解释:比赛中有两支队伍。 grid[0][1] == 1 表示 0 队比 1队强。所以 0 队是冠军。
示例 2:
输入:grid = [[0,0,1],[1,0,1],[0,0,0]]
输出:1
解释:比赛中有三支队伍。 grid[1][0] == 1表示 1 队比 0 队强。 grid[1][2] == 1 表示 1 队比 2 队强。 所以 1 队是冠军。
提示:
n = = g r i d . l e n g t h n == grid.length n==grid.length
n = = g r i d [ i ] . l e n g t h n == grid[i].length n==grid[i].length
2< = n < = 100 2 <= n <= 100 2<=n<=100
g r i d [ i ] [ j ] grid[i][j] grid[i][j] 的值为 0 0 0 或 1 1 1
对于满足 i ! = j i != j i!=j 的所有 i , j i, j i,j , g r i d [ i ] [ j ] ! = g r i d [ j ] [ i ] grid[i][j] != grid[j][i] grid[i][j]!=grid[j][i] 均成立
生成的输入满足:如果 a 队比 b 队强,b 队比 c 队强,那么 a 队比 c 队强
分析:
这个题目,因为如果 g r i d [ i ] [ j ] = = 1 grid[i][j] == 1 grid[i][j]==1,那么 i i i队比 j j j 队强,那么我们需要找到冠军队伍,则 冠军队伍 i i i的 g r i d [ i ] [ j ] = = 1 grid[i][j] == 1 grid[i][j]==1对所有的 j ( j ! = i ) j(j!=i) j(j!=i)恒成立,所以只要找到一个满足该条件的队伍,即是答案。
代码:
一场比赛中共有 n 支队伍,按从 0 到 n - 1 编号。每支队伍也是 有向无环图(DAG) 上的一个节点。
给你一个整数 n 和一个下标从 0 开始、长度为 m 的二维整数数组 edges 表示这个有向无环图,其中 edges[i] = [ui, vi] 表示图中存在一条从 ui 队到 vi 队的有向边。
从 a 队到 b 队的有向边意味着 a 队比 b 队 强 ,也就是 b 队比 a 队 弱 。
在这场比赛中,如果不存在某支强于 a 队的队伍,则认为 a 队将会是 冠军 。
如果这场比赛存在 唯一 一个冠军,则返回将会成为冠军的队伍。否则,返回 -1 。
注意
环 是形如 a1, a2, …, an, an+1 的一个序列,且满足:节点 a1 与节点 an+1 是同一个节点;节点 a1, a2, …, an 互不相同;对于范围 [1, n] 中的每个 i ,均存在一条从节点 ai 到节点 ai+1 的有向边。
有向无环图 是不存在任何环的有向图。
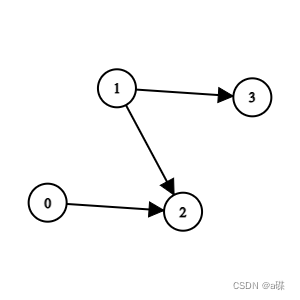
输入:n = 3, edges = [[0,1],[1,2]]
输出:0
解释:1 队比 0 队弱。2 队比 1 队弱。所以冠军是 0 队。
输入:n = 4, edges = [[0,2],[1,3],[1,2]]
输出:-1
解释:2 队比 0 队和 1 队弱。3 队比 1队弱。但是 1 队和 0 队之间不存在强弱对比。所以答案是 -1 。
提示:
1< = n < = 100 1 <= n <= 100 1<=n<=100
m = = e d g e s . l e n g t h m == edges.length m==edges.length
0< = m < = n ∗ ( n − 1 ) / 2 0 <= m <= n * (n - 1) / 2 0<=m<=n∗(n−1)/2
e d g e s [ i ] . l e n g t h = = 2 edges[i].length == 2 edges[i].length==2
0< = e d g e [ i ] [ j ] < = n − 1 0 <= edge[i][j] <= n - 1 0<=edge[i][j]<=n−1
e d g e s [ i ] [ 0 ] ! = e d g e s [ i ] [ 1 ] edges[i][0] != edges[i][1] edges[i][0]!=edges[i][1]
生成的输入满足:如果 a 队比 b 队强,就不存在 b 队比 a 队强
生成的输入满足:如果 a 队比 b 队强,b 队比 c 队强,那么 a 队比 c 队强
分析:
相比于第一题是利用矩阵给出强弱关系,本题是直接给出图中每一条边,来代表强弱关系。其实和第一题思考方式一致,如果存在答案,那么最强的队伍,即冠军队伍是不可能存在一条边指向它的,即入度为0。那么我们只需要判断入度为0的点是不是有且仅有一个即可。
代码:
有一棵 n 个节点的无向树,节点编号为 0 到 n - 1 ,根节点编号为 0 。给你一个长度为 n - 1 的二维整数数组 edges 表示这棵树,其中 edges[i] = [ai, bi] 表示树中节点 ai 和 bi 有一条边。
同时给你一个长度为 n 下标从 0 开始的整数数组 values ,其中 values[i] 表示第 i 个节点的值。
一开始你的分数为 0 ,每次操作中,你将执行:
选择节点 i 。
将 values[i] 加入你的分数。
将 values[i] 变为 0 。
如果从根节点出发,到任意叶子节点经过的路径上的节点值之和都不等于 0 ,那么我们称这棵树是 健康的 。
你可以对这棵树执行任意次操作,但要求执行完所有操作以后树是 健康的 ,请你返回你可以获得的 最大分数 。
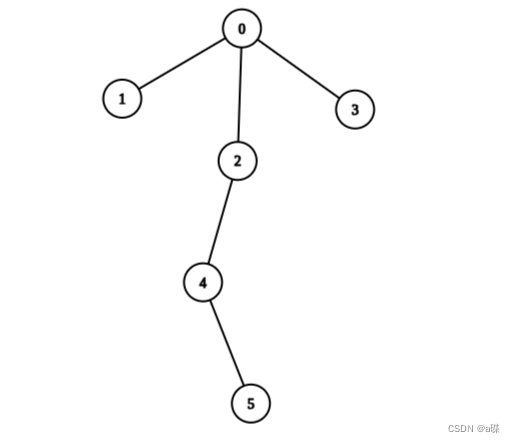
输入:edges = [[0,1],[0,2],[0,3],[2,4],[4,5]], values = [5,2,5,2,1,1]
输出:11
解释:我们可以选择节点 1 ,2 ,3 ,4 和 5 。根节点的值是非 0 的。所以从根出发到任意叶子节点路径上节点值之和都不为0 。所以树是健康的。你的得分之和为 values[1] + values[2] + values[3] + values[4] +values[5] = 11 。 11 是你对树执行任意次操作以后可以获得的最大得分之和。
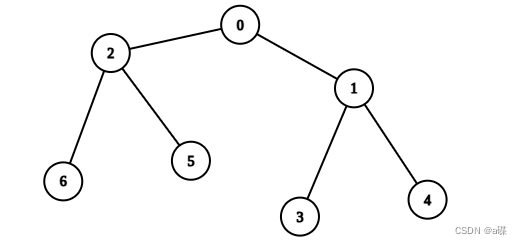
输入:edges = [[0,1],[0,2],[1,3],[1,4],[2,5],[2,6]], values =
[20,10,9,7,4,3,5]
输出:40
解释:我们选择节点 0 ,2 ,3 和 4 。
所以树是健康的。你的得分之和为 values[0] + values[2] + values[3] + values[4] = 40 。 40 是你对树执行任意次操作以后可以获得的最大得分之和。
提示:
2< = n < = 2 ∗ 1 0 4 2 <= n <= 2 * 10^4 2<=n<=2∗104
e d g e s . l e n g t h = = n − 1 edges.length == n - 1 edges.length==n−1
e d g e s [ i ] . l e n g t h = = 2 edges[i].length == 2 edges[i].length==2
0< = a i , b i < n 0 <= ai, bi < n 0<=ai,bi
1< = v a l u e s [ i ] < = 1 0 9 1 <= values[i] <= 10^9 1<=values[i]<=109
输入保证 edges 构成一棵合法的树。
分析:
一个树形DP的题目,因为取出一个点的 v a l u e value value之后,该点的 v a l u e value value会变成0,又有条件,从根节点出发,到任意叶子节点经过的路径上的节点值之和都不等于 0 ,那么我们称这棵树是健康的。为了达到健康的目的,我们需要判断当前结点选or不选所带来的影响。
怎样保证下面的结点至少有一个点被选呢, a n s 1 ans1 ans1的值其实就是选了点的情况,那么如果走到了叶子节点,那么叶子结点的值肯定不选。因为叶子节点的前驱节点 p r e pre pre,如果选择了 p r e pre pre(走到了 p r e pre pre,说明前面的结点肯定都选择了),则其叶子节点肯定不能选。如果没有选择 p r e pre pre,那么上一层递归中的 a n s 1 = s u m [ p r e ] ans1 = sum[pre] ans1=sum[pre]包含了叶子结点的值。所以不管怎样都不选择叶子节点,也满足了树要健康的要求。
sum数组记录了每一个结点的子树中的value的和(不包括当前结点),也可以用一个dfs进行计算。
代码:
class Solution { public: long long maximumScoreAfterOperations(vector给你一个下标从 0 开始的整数数组 nums 。
nums 一个长度为 k 的 子序列 指的是选出 k 个 下标 i_0 < i_1 < … < i_{k-1} ,如果这个子序列满足以下条件,我们说它是 平衡的 :
对于范围 [1, k - 1] 内的所有 j , n u m s [ i j ] − n u m s [ i j − 1 ] > = i j − i j − 1 nums[i_j] - nums[i_{j-1}] >= i_j - i_{j-1} nums[ij]−nums[ij−1]>=ij−ij−1都成立。
nums 长度为 1 的 子序列 是平衡的。
请你返回一个整数,表示 nums 平衡 子序列里面的 最大元素和 。
一个数组的 子序列 指的是从原数组中删除一些元素(也可能一个元素也不删除)后,剩余元素保持相对顺序得到的 非空 新数组。
示例 1:
输入:nums = [3,3,5,6]
输出:14
解释:这个例子中,选择子序列 [3,5,6] ,下标为 0 ,2 和 3 的元素被选中。nums[2] - nums[0] >= 2 - 0 。 nums[3] - nums[2] >= 3 - 2 。所以,这是一个平衡子序列,且它的和是所有平衡子序列里最大的。 包含下标 1 ,2 和 3 的子序列也是一个平衡的子序列。 最大平衡子序列和为14 。
示例 2:
输入:nums = [5,-1,-3,8]
输出:13
解释:这个例子中,选择子序列 [5,8] ,下标为 0 和 3 的元素被选中。nums[3] - nums[0] >= 3 - 0 。 所以,这是一个平衡子序列,且它的和是所有平衡子序列里最大的。 最大平衡子序列和为13 。
示例 3:
输入:nums = [-2,-1]
输出:-1
解释:这个例子中,选择子序列 [-1] 。 这是一个平衡子序列,而且它的和是 nums所有平衡子序列里最大的。
提示:
1< = n u m s . l e n g t h < = 1 0 5 1 <= nums.length <= 10^5 1<=nums.length<=105
− 1 0 9 < = n u m s [ i ] < = 1 0 9 -10^9 <= nums[i] <= 10^9 −109<=nums[i]<=109
分析:
对于每一个长度为k的子序列,需要满足对于范围 [ 1 , k − 1 ] [1, k - 1] [1,k−1]内的所有 j j j, n u m s [ i j ] − n u m s [ i j − 1 ] > = i j − i j − 1 nums[i_j] - nums[i_{j-1}] >= i_j - i_{j-1} nums[ij]−nums[ij−1]>=ij−ij−1都成立。我们可以转换一下变成 n u m s [ i j ] − i j > = n u m s [ i j − 1 ] − i j − 1 ( i > j ) nums[i_j] - i_j >=nums[i_{j-1}] - i_{j-1} \ (i > j) nums[ij]−ij>=nums[ij−1]−ij−1 (i>j)。所以我们可以令序列 b [ i ] = n u m s [ i ] − i b[i] = nums[i] - i b[i]=nums[i]−i,则我们要得到的这个子序列 b [ i ] b[i] b[i]是一个非严格递增子序列。对于所有满足条件的序列 b b b,要得到一个 s u m ( n u m s ) sum(nums) sum(nums)最大的子序列。
我们定义 f [ i ] f[i] f[i]表示子序列的最后一个数的下标为i时,对应的元素和最大的值,那么最后的答案就是 m a x ( f ) max(f) max(f)。
状态转移方程为 f [ i ] = m a x j m a x ( f [ j ] , 0 ) + n u m s [ i ] f[i] = max_{j}\ max(f[j],0) + nums[i] f[i]=maxj max(f[j],0)+nums[i]。
j< i j < i j
代码:
class Solution { public: int bitset(int x){ return x & -x; } long long maxBalancedSubsequenceSum(vector