小波混沌神经网络是一种神经网络模型,结合了小波变换和混沌理论,用于信号处理、分类和预测。该模型基于多层前向神经网络,其中每一层由小波基函数和一个非线性混沌函数构成。
一、小波混沌神经网络模型选用由小波函数组成的小波暂态混沌神经网络作为研究对象。在连续Hopfield网络中引入小波理论和暂态混沌构造的小波混沌神经网络定义如下
对于Hopfield网络可以看我之前的文章
混沌系统在图像加密中的应用(Hopfield混沌神经网络)

与 Hopfield 神经网络相 比,此小波混沌神经网络的激励函数由小波函数和 Sigmoid 函数组成,且具有暂态的混沌动力学行为。其激励函数是非单调递增但总体上是递增的函数,是由 Sigmoid 函数和 Wavelet 函数组合而成的。
Wavelet 函数的意义是既能使激励函数非单调,又能使激励函数有小波函数的优点。其混沌产生机制是通过自反馈连接项按指数方式递减引入的。且此网络多增加了一项非线性时变衰减项
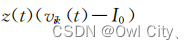
当自反馈连接权 z(t) 以指数方式趋于零时,此混沌神经网络退化为一个 Hopfield 神经网络
为了更好地分析上述模型的运行机理,以单个神经元为例(令α=0),分析混沌 Hopfield 神经网络的动力学特性。我们选取的激活函数为sigmoid+Wavelet函数,设置网络参数分别为:
ε_1 = 0.035
ε_2 = 0.1
c = 1/7
k = 1.0
u_0 = 0.5
z_0 = 0.8
I_0 = 0.6
β = 0.001
则网络的输出 v(t)、退温函数z(t)的演化过程分别如下图所示。由图,该网络具有暂态混沌动力学行为,随 着z(t) 不断衰减,通过一个倍周期逆分岔的连续混沌分岔过程,网络将逐渐趋近于一个稳定的平衡点。
二、拓展大家可以试试其他激活函数,比如softPlus、arcTan、softsign、bent_identity、symmetrical_sigmoid、log_log、gauss、Morlet、ReLU、P-ReLU、Leaky-ReLU、Maxout 等等
三、python代码 import numpy as np import matplotlib.pyplot as plt import pylab as mpl mpl.rcParams['font.sans-serif'] = ['YouYuan'] # 指定默认字体 def sigmoid(x): return 1. / (1 + np.exp(-x)) def Morlet(x): return np.exp(-((x)**2) / 2) * np.cos(5 * x) def Wave(u_t0, z0): v_t = sigmoid((u_t0 / r1)) + c * Morlet((u_t0 / r2)) u_t = k * u_t0 - z0 * (v_t - I0) z_t = (1 - b) * z0 return v_t, u_t, z_t list_vt = [] list_ut = [] list_I0 = [] list_zt = [] list_rt = [] list_time = [] # 系统初值 z0 = 0.8 u_t0 = 0.5 # 系统参数 r1 = 0.035 r2 = 0.1 c = 1 / 7 # 0

