最近论文中常常接触到激光产生混沌的方程，激光器作为非线性元件，在信息处理中具有非常大的潜力，其中激光产生混沌应用在通信中很有用处。论文中对于模拟数据部分，采用了以下公式来产生混沌：
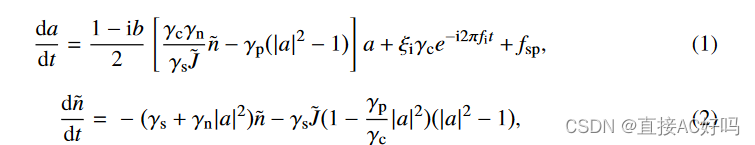
以此公式产生混沌的方法应用于模拟数据中的论文，单我看到的已经不下五篇了。对于使用怕python将其产生的混沌运行出来，自己也在尝试。但是得到的结果并不如意。文章中使用的是二阶龙格库塔（second-order Runge-Kutta）的方法来对这两个式子进行积分。以下是我对于二阶龙格库塔方法解方程的步骤（手写是因为到现在还是不会用csdn来编辑公式）
对于fsp也就是朗格万项的理解确实不够，自己在以后也会精进一下理解，这里把它看成一个常数项进行处理。
对于n~的微分公式的积分并没有采用二阶龙格塔库积分方法，而是通过直接求出原式带入到1式子中。我对于整个解微分方程的python代码书写如下（实验参数已经标注在开头）：
import matplotlib.pyplot as plt import math rc=5.36*1e11 rs=5.96*1e9 rn=7.53*1e9 rp=1.91*1e10 b=3.2 J=1.222 fr=1e10 oi=0.05 fi=8*1e9 h=1.19*(1/1e12) chaotic_value=[] def value_A(a): aa=abs(a) anss=(rs+rn*aa*aa)*(-1.0) return anss def value_B(a): aa=abs(a) anss=rs*J*(1-(rp/rc)*aa*aa)*(aa*aa-1)*(-1.0) return anss def value_n(t,a): anss=(math.exp(value_A(a)*t)-value_B(a))/value_A(a) return anss def value_f(t,a): aa=abs(a) first=complex(1,b*(-1))/2.0 second=(((rc*rn*value_n(t,a))/(rs*J))-rp*(aa*aa-1))*a third=oi*rc*complex(math.cos(2*math.pi*fi*t),(-1)*math.sin(2*math.pi*fi*t)) forth=((4.0*math.pi*10.0*1e6)/(1+b*b))**0.5 anss=first*second+third+forth return anss t=0.0 y=0.0 chaotic_value.append(y) for item in range(100): k1=value_f(t,y) k2=value_f(t+h,y+h*k1) y_next=y+h*((k1+k2)/2.0) chaotic_value.append(y_next) y=y_next t=t+h pass for item in chaotic_value: print(item) plt.plot(range(101),chaotic_value) plt.show()
值得注意的是式子中的i应该是复数的虚部，而一开始我认为是当前的步数。得出的结果更加离谱。下面是取样50个点运行的图像：
下图为100个点：
接下来是10000个点
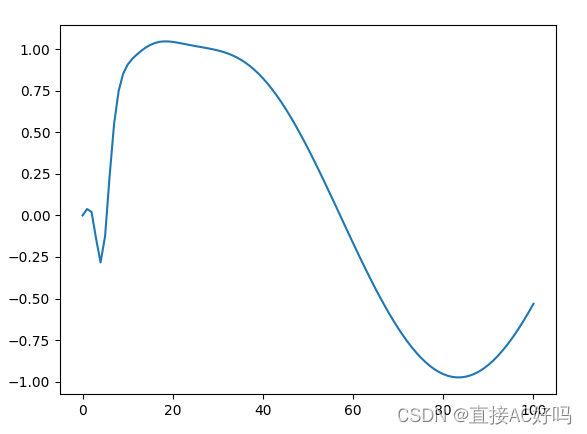
最终产生的混沌图像应该是什么样子我也没有见过，但是我感觉我形成的这一个图像过于规律了，不想混沌，但是我也是通过文章表述来编写的代码，debug了挺长时间。很希望专业认识对于这一混沌产生函数的代码编写进行指正。或者是有哪里理解的不对，欢迎交流。感觉以后写论文肯定会用到这个模型的。希望佬们快快帮帮我。
相关论文链接：https://opg.optica.org/oe/fulltext.cfm?uri=oe-31-24-40592&id=542433
